Ranking by medians

Australian Universities' Review, Volume 83, Number 1, 2016, pp. 62-64

pdf of article

Brian Martin

When a committee needs to rank applications, it is worthwhile having committee members independently rank the applications and then starting the committee’s discussion with the medians of the ranks.

It was time to rank PhD scholarship applications in the faculty. I joined the large committee, with one representative from each department. The meeting was rancorous and lasted so long it had to be reconvened at a later time to finish the ranking.

The meeting was difficult for several reasons. Each committee member came to the meeting with a preferred order in mind, but no one knew where everyone else stood. Some members were playing favourites, presenting arguments for their desired applicants: they would emphasise some positive attribute of an applicant and ignore negatives that may have influenced others, with the positives and negatives being raised or downplayed in a selective fashion. Finally, some members were more forceful than others. The meeting eventually ended, but left a bitter taste for many who participated.

A few years later, I became chair of the committee and tried a new system that overcame many of the previous problems. The meetings for ranking scholarships and grant applications were shorter and less contentious. I call the method used “ranking by medians.” It is currently used at the University of Wollongong for ranking scholarships at the university level.

How it works

Before the meeting, each committee member independently rates each application according to selection criteria, for example with a score between 0 and 100. The key, though, is not the score but the ranking of applications. If there are 20 applications, each committee members ranks them 1 to 20. Alternatively, ranks can be readily derived from the scores.

The scores and ranks are given to an assistant who prepares a table listing each applicant’s rank as assessed by each committee member. Then the median rank for each application is calculated. The median is just the middle of a group of numbers. For example, if the five ranks are 1, 1, 2, 5 and 11, the median is 2. (The average in this case is 4.) With a small committee, it’s easy to calculate the median by eye; with a large committee, a spreadsheet function can be used.

Committee members then attend a meeting, and the table of ranks is given to each member and/or projected on a screen, with applicants ordered in terms of the median ranks for their applications. Then the committee members can discuss whether to use the median ranks as the basis for awarding scholarships (or whatever), or to change the order.

In my experience, this method makes decision-making much easier. There is seldom disagreement about the upper or lower ranked applications, so most discussion is about those at the boundary.

Why it works

Independent ranking is a crucial part of this method. Independent rankings reduce the influence of dominant personalities. Each member’s assessment is included, regardless of how forceful or retiring they are. Indeed, a member can be absent from the meeting yet still have a nearly as much influence on the outcome as others. Independent assessments are vital in taking advantage of what has been called the ‘wisdom of crowds’ (Surowiecki, 2004). Individuals may vary greatly in their assessments but when combined the result can be surprisingly accurate. Indeed, a large diverse committee with less expertise is likely to perform better than a small one with more expertise (Page, 2007).

Why use the median rank, rather than the average score? The trouble with averages is that they can be easily skewed by outliers. A committee member can manipulate the outcome, consciously or unconsciously, by awarding an extremely high score to a favoured applicant or a low one to a detested one. The median, in contrast, mutes the effect of outliers. Suppose four committee members give scores of 95, 95, 94 and 90, but the fifth member gives a score of 40, dramatically bringing down the average. The medians might be 1, 1, 2, 4 and 11 (as before). Even if the fifth committee member’s rank is 99 rather than 11, it makes no difference to the median rank, which is still 2. Mathematically, the median is more robust than the average.

There is one other powerful effect in this process: every committee member can see every other member’s rankings. It becomes harder to play favourites. Explicit independent rankings make special pleading and attempts to game the system more obvious and easier to resist.

An example

Suppose there are five applications, A, B, C, D and E, and four committee members, M1, M2, M3 and M4.

Each committee member ranks the applications, which means putting them in priority order. Suppose they give these rankings:

It looks confusing! So let’s prepare a table with the rankings. The top-ranked application for M1 is A, so A gets a 1, B gets a 2 and so forth.

The median in each case is the average of the second and third highest ranking. The four rankings for A are 1, 1, 2, 5. The second highest is 1 and the third highest is 2, so the median is 1.5. (With an odd number of committee members, the median is the middle ranking.) Note that I set up the table so that the applications are in order of the medians. Usually they won’t be so neatly ordered, so then it’s a simple matter of sorting by median. In this example M4 has a very different perspective than the other committee members, but this has only a minor effect on the medians and almost none on the final order.

In some committees I’ve attended using this system, we are given a table just like that one above, with all the rankings by each committee member, but no names of committee members attached, though it’s sometimes possible to infer them. In this way everyone can see how each committee member ranked the applications, without getting too personal. It’s a useful basis for the subsequent discussion. For example, if there are dramatic differences in rankings of one or more applications, this can lead to a discussion of the assessment criteria. The medians are not determinative, but a good argument is needed to go strongly against them.

Final comment

In many cases, decisions about applications for jobs, scholarships and grants may be best made by combining measures such as test scores and publication records (Dawes, 1979). However, academics are reluctant to relinquish their role in making academic judgements despite evidence that other measures are more effective. When academic judgements are required or desired, ranking by medians by a large and diverse group making independent assessments is a worthwhile option.

Appendix: Technicalities

If someone ranks two applications as equal, their ranks should be the average of the two. For example, if two applications are ranked equal first, they should each be given a rank of 1.5 (the average of 1 and 2); the next application will be rank 3.

Sometimes committee members judge some applications to be uncompetitive and do not bother to rank them. These applications should be given the average of the bottom ranks. If out of 20 applications, a committee member ranks only the top 10, then each of the remaining applications should be ranked 15.5 (the average of 11, 12 … 20).

It is a different matter when a committee member does not want to rank an application because of a conflict of interest. Giving this application a low rank would be unfair: it might actually be the committee member’s favourite. There are two options. One is to say, go ahead and rank them all regardless of conflicts of interest, because with medians the impact of bias will be limited. The other option is to renormalise all the ranks for this committee member: the ‘increment’ for each ranked application should be (N+1)/(n+1), where N is the number of applications and n is the number ranked. This ensures that the median of ranked applications remains the same no matter how many are ranked. This renormalisation can also be used when a committee member does not evaluate one or more applications due to an oversight or administrative error.

The following table gives the result for N=11, rounded to the nearest 0.1. When 10 of the 11 are ranked, n=10, and so forth.

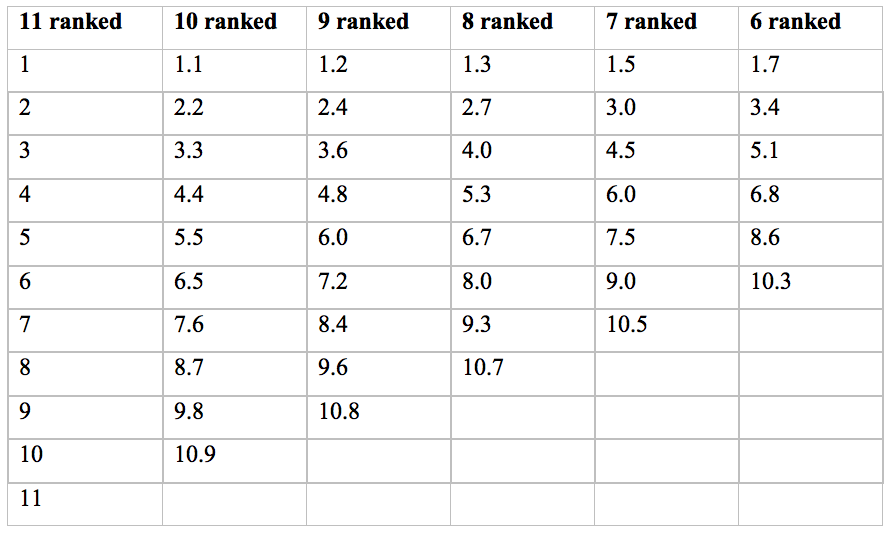
For example, suppose, due to conflicts of interest, a committee member ranks only 8 of the 11 applications. The highest ranked application is given a rank of 1.3, the next highest 2.7, etc.

Acknowledgements

I thank Lyn Carson, Leonie Clement, Tim Marchant, Anne Melano, Linda Steele and Graham Williams for useful feedback.

References

Dawes, Robyn M. (1979). "The robust beauty of improper linear models in decision making," American Psychologist, 34 (7), 571-582.

Page, Scott E. (2007). The Difference: How the Power of Diversity Create Better Groups, Firms, Schools, and Societies. Princeton, NJ: Princeton University Press.

Surowiecki, James (2004). The Wisdom of Crowds. New York: Doubleday.

Go to

Brian Martin's publications on education

Brian Martin's publications

Brian Martin's website